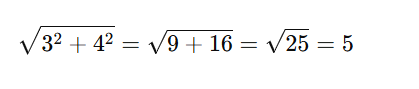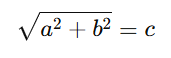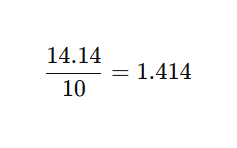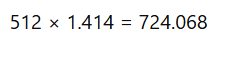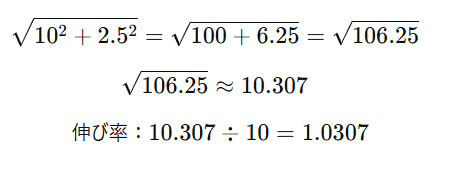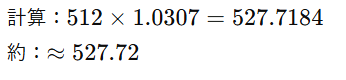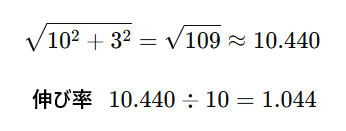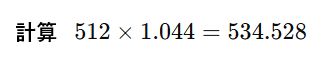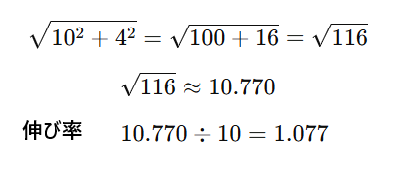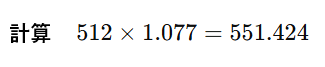こんにちは。
代表の佐藤哲郎です。
中学数学が役立つ!勾配天井・屋根の開口寸法と煙突施工
薪ストーブの煙突を勾配天井や屋根に通す場合、ただ丸く開ければいいわけではありません。
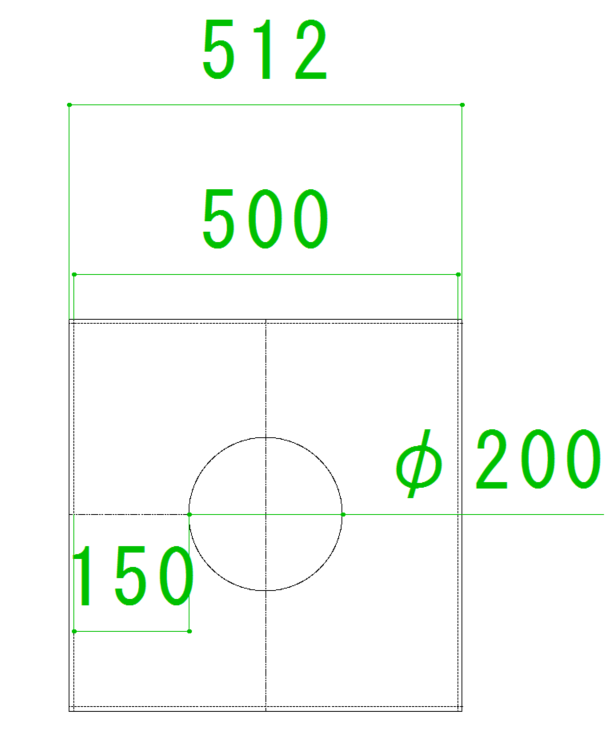
実際の施工では「512角」で開口します。さらに屋根や天井に勾配があると、正方形ではなく「長方形」に寸法を出す必要があります。
ここで役立つのが、中学3年生で習う三平方の定理。この記事では、施工の現場で使える寸法の出し方をわかりやすく解説します。
なお、今回の記事は既存住宅の屋根煙突工事|薪ストーブ設置に必要な全工程と注意点
の補足となる内容です。
なぜ円形でなく角形(512角)で開口するのか
こちらの記事のおさらいです。
理由は、
1、四角形の方が補強がしやすい
2、煙突外周部と開口端部の離隔距離を150mmにするのが弊社の基本ルール
です。
二重煙突が直径200mm、開口端部が500mmですので150mmとなります。
12mmというのは両端に取り付ける6mmのケイカル板です。
絵にすると以下のようになります。
それでは、なぜ煙突外周部と開口端部の離隔距離を150mmとしているのかを踏み込んでみましょう。
国土交通省が定める
『建築基準法施行令第百十五条第一項第一号から第三号までの規定を適用しないことにつき防火上支障がない煙突の基準を定める件』
の三 イに以下の文言があります。
『先端を下向きにした煙突にあつては、その排気のための開口部の各点からの水平距離が十五センチメートル以内で~』
……なんとも読みにくい文章ですよね。(お役所の文書って、どうしてこんなに硬いんでしょうか…笑)
要するにここで言っているのは、「煙突の外周部と開口端部は15センチ=150mm以上離しておくべき」ということです。
建築基準法や関連告示には、煙突の周囲の防火上の基準は定められていますが、実は「シングル煙突」や「二重断熱煙突」といった呼称も、その離隔距離の数値も法律上は明確に定義されていません。
つまり、現場で一般的に使われている「シングル」「二重」といった区別はあくまで業界内の便宜的な呼び方であり、法的な基準そのものではないのです。
こうした法規のあいまいさを踏まえ、弊社では安全を最優先に考え、断熱二重煙突を使用する場合でも外周部から開口端部まで150mm以上の離隔距離を確保することを標準としています。
これは法律の最低基準にとどまらず、火災リスクを限りなく減らし、お客様に安心して薪ストーブをご利用いただくための弊社独自の安全基準です。
勾配があると開口はどう変わる?
それでは、勾配天井や屋根の野地板に512mm×512mmで開口しよう、、、
これをやると後々困ることになります。
その理由を図解でご説明します。
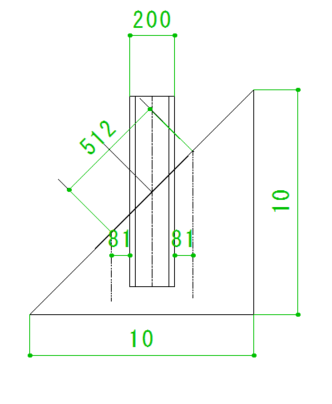
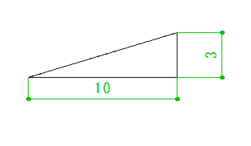
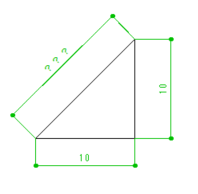
まず、勾配がついている箇所を512mmで開口した場合です。
分かりやすいように矩勾配(10寸勾配)を例にしました。
勾配がある箇所を510mmで開口してしまうと、煙突外周部と木枠との離隔距離は81mmになってしまいます。
こうなるのは、角度があると水平距離はその角度の分だけ伸びるからです。
つまり、斜めの屋根にまっすぐな煙突を通すと、思ったよりも広く穴を開けないといけない、ということです。
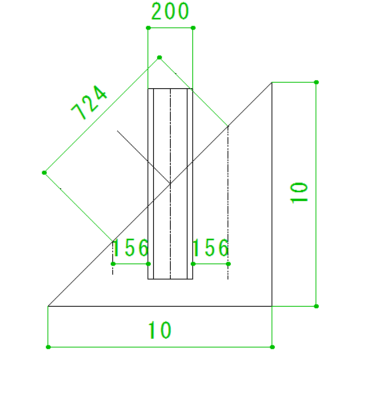
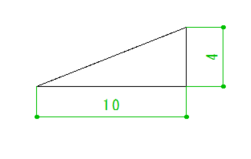
それでは、煙突外周部と木枠との水平距離を156mmにする場合の開口寸法はいくつになるでしょうか?
先に答えをお伝えすると、正解は724mmです。
この724mmと言う開口寸法がどのように算出されたかを次の章でご説明します。
(すこし眠くなるかもしれません笑)
三平方の定理で寸法を出す
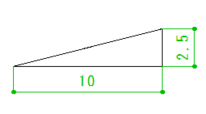
まず大前提として屋根の勾配に2.5寸、3寸、4寸とあらゆる勾配があります。
これの意味は水平距離で10進んだらいくつ垂直に上がるかということになります。
矩勾配といわれるものは水平距離に10進んだら10垂直に上がります。
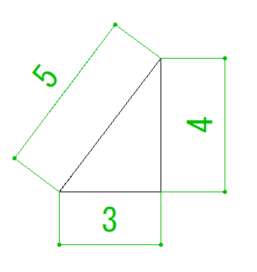
既にお気づきかもしれませんが、点と点を線で結ぶと直角三角形が描けます。
それぞれの勾配で見てみましょう。
勾配が上がるほど、水平距離の伸び寸法は長くなります。
それでは、どうやって伸び寸法を算出すればいいでしょうか?
ここで役に立つのが中学3年生で習う
『三平方の定理』または『ピタゴラスの定理』
です。
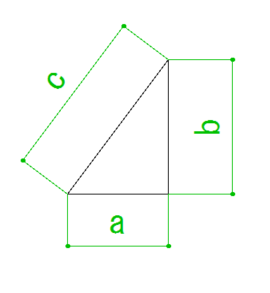
これは
『直角三角形の底辺(隣辺)の長さの二乗と垂直(対辺)の長さの二乗を足した平方根が斜辺の長さになる』
と言うものです。
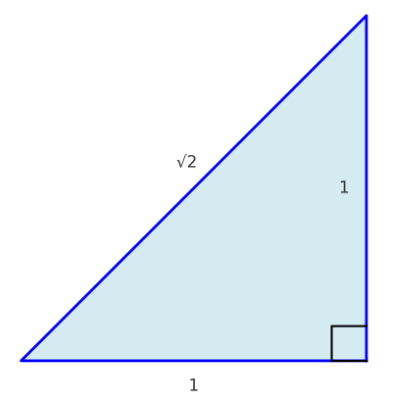
たとえば、3の二乗+4の二乗=5の二乗、というあの有名な三角形の話です。
実際に図解でご説明しましょう。
√や平方根と聞くと、そろそろ眠くなりましたでしょうか?笑
大丈夫です。慣れればとても便利な道具になります笑
このピタゴラスと言う天才が編み出した定理を応用して伸びを計算します。
現場での実務
それでは実際に勾配と実際の伸び寸法を前述した矩勾配(10寸勾配)を例に計算してみましょう。
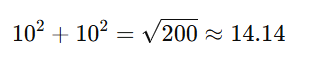
14.14…と算出されましたね。
しかし、まだ勾配の開口寸法は出ていません
ここで、水平10に対しての伸び率を計算します。
勾配14.14・・・を水平10で割ると
1.414が矩勾配における水平距離の伸び率となります。
開口寸法512に上記の伸び率をかけると
勾配の開口は724になりました。
先程の図面と同じ寸法になりましたね。
ちなみに、矩勾配の場合水平と垂直の寸法が同じなので直角二等辺三角形になります。
三平方の定理より、それぞれの辺の比は以下のようになります。
それでは、前述した2.5寸、3寸、4寸についても同じように計算してみましょう。
■2.5寸勾配
■3寸勾配
■4寸勾配
他の勾配についても全く同じ計算式です。
ここまでご覧になって
『ネットで調べたらchatGPTに聞けばいいんじゃないの?』
と思われますよね?
確かにそのとおりです。検索すれば答えはヒットします。
しかし、電波が非常に悪い別荘地ですとネットに繋がらず、調べることができません。
ですので、自力で計算する術を習得していれば、電卓があれば計算できます。
まとめ
学生時代、数学を勉強したところで何の役に立たないと、何度も思いました。
しかし、この仕事を始めてから数学はとても便利な道具であるとつくづく感じます。
私は学生時代、全く勉強しませんでした。
数学は40歳になってから学びなおし、中学3年生までの技能が問われる数学検定3級まで取りました。
実務で使う数学は検定の問題よりずっと簡単です。
どう応用できるかがポイントになります。
仕事に活かせると、学問って本当に楽しいものだと感じられます。
このコラム記事が皆様のお役に立てれば幸いです。
弊社薪ストーブ導入の際、ご相談いただく場合は以下のボタンをクリック(タップ)してください。
それでは今日はこの辺で失礼したいと思います。
どうもありがとうございました。